cv,cg相关概念

相机校正 Camera Calibration

前言

从这里开始是研究现实世界转化到屏幕空间的关系，注意和图形学分别开

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数

Camera Calibration简单来说就是求解世界空间到像素空间的过程，也就是求解最终的投影矩阵的过程

坐标系 （coordinate system）

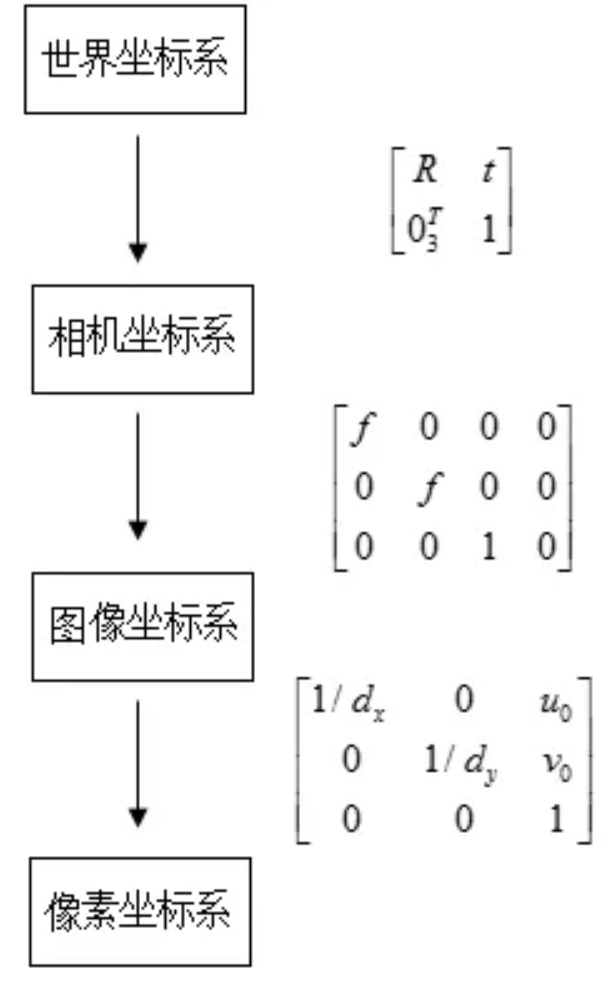
世界坐标系、相机坐标系、图像坐标系、像素坐标系

标定 （calibration）

使用棋盘作为标定物，二维物体相对于三维物体会缺少一部分信息，于是多次改变棋盘的方位来捕捉图像。

1. 从世界坐标系到相机坐标系

旋转平移矩阵

2. 相机坐标系到理想图像坐标系

相似三角形

3. 理想图像坐标系到实际图像坐标系

Radial Distortion (径向畸变)

• 光线经过透镜的边缘时，其弯曲程度比在透镜的中心为大
• distortion的情况在透镜越小时越明显
• 可以通过泰勒级数展开式来校正（k1,k2,k3）

Tangential Distortion (切向畸变)

• 成像仪被贴上摄像机的时候，误差使得影像平面和透镜不完全平行，从而产生切向畸变
• 如果一个矩形被投影到成像仪上时，可能会变成一个梯形
• 使用 (p1,p2)来校正

从实际图像坐标系到像素坐标系

平移，并且适应分辨率

新视角合成 Novel View Synthesis

新视角合成任务(Novel view synthesis)指的是给定源图像(src image)和源姿态(src pose),以及目标姿态(Target pose)，渲染生成目标姿态对应的图片 (Target image)

源姿态

从相机坐标系转化到世界坐标系的变换矩阵

从机器学习的角度理解：从一些<图片，相机矩阵>构成的训练集中模型，测试时给一个训练集中没有的相机矩阵，模型能预测出对应的图片

SfM(Structure from Motion)

• 是一种三维重建的方法，用于从motion中实现3D重建
• 从时间系列的2D图像中推测出3D信息

最优化 (Optimization)

泛指定量决策问题，主要关心如何对有限资源进行有效分配和控制，并达到某种意义上的最优

TBR (tile-based rendering)

GPU的Tile-Based架构

所谓Tile，就是将几何数据转换成小矩形区域的过程。光栅化和片段处理在每Tile的过程中进行。Tile-Based Rendering的目的是在最大限度地减少fragment shading期间GPU 需要的外部内存访问量,从而来节省内存带宽。TBR将屏幕分成小块，并在将每个小图块写入内存之前对每个小图块进行片段着色。为了实现这一点，GPU 必须预先知道哪些几何体属于这个tile.因此，TBR将每个渲染通道拆分为两个处理通道：

• 第一遍执行所有与几何相关的处理，并生成该tile专属的Primitive list，指示哪些图元在tile内。
• 第二遍逐tile进行光栅化并且进行Fragment shading，并在完成后将其写回内存。

方便了部分算法的实现

TBR启用了一些算法，否则这些算法的计算成本太高或带宽使用过高。

tile足够小，于是可以在内存中本地存储足够多的sample，以实现MSAA。因此，硬件可以在tile写回内存期间将多个样本resolve，而无需单独的resolve pass。

传统的Defer-Rendering将使用多渲染目标 (MRT) 渲染来实现延迟照明，将每个像素的多个中间值写回主内存，然后在第二遍中重新读取它们。而在TBR中片段着色器以编程方式访问由先前片段存储在帧缓冲区中的值可以对Defer-Rendering进行优化。

Point Cloud

A point cloud is a discrete set of data points in space. (三维图像)

ray marching

• 对于某些效果使用参数化描述，难以使用三角面片描述，使用ray marching能够解决这些问题
• ray marching按照摄像机方向(Ray)逐步前进(Marching)进行采样，是以迭代方式进行采样的

距离场

按距离物体表面最小距离进行迭代的步进

如果出现某些射线在步进一次并没有达到表面时，可以以此时距离物体的距离场再次按照原方向进行步进。如果某条线在步进多次后一直逐渐远离，也就是说明这根射线永远无法与物体相交，如果一根射线在步进多次后距离场的值越来越小，如果设值为0.01，那么就可以确定这个点的位置就是物体表面。

SDF有向距离场

描述空间中任意一个点到达物体最近的距离

gradient descent optimization 梯度下降优化算法

gradient

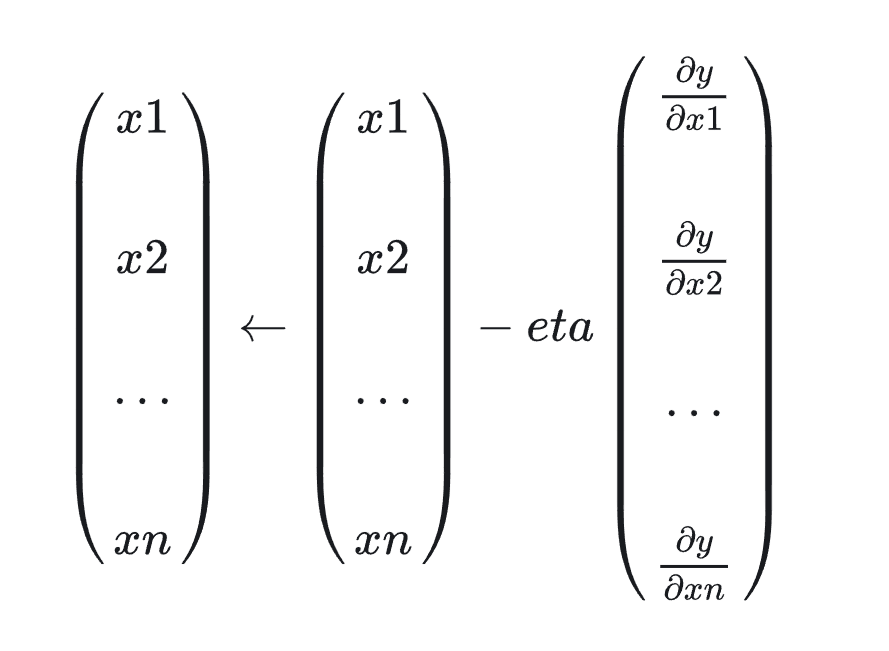
沿梯度的负方向的函数值下降最快的方向

eta 学习率

$x \gets x - eta \cdot \frac {df(x)} {dx}$

让 $x$减去$eta$乘以函数的导数

多元函数的梯度下降

rotation quaternion 四元数

Euler rotation

缺点：

1. 这种方法是要按照一个固定的坐标轴的顺序旋转的，因此不同的顺序会造成不同的结果
2. 欧拉旋转有父子层级，当中间层级的坐标轴旋转超过一定的范围时，导致中层和外层坐标轴重合，产生万向死锁(Gimbal Lock)
3. Gimbal Lock会导致Euler Rotation无法实现球面平滑插值

quaternion 四元数

$q = w + x \cdot i + y \cdot j + z \cdot k$

其中：

$i^2 = j^2 = k^2 = -1$

$ij = -ji = k$

$jk = -kj = i$

$ki = -ik = j$

三维空间中的旋转可以被认为是一个函数 $\phi$，从 $\mathbb{R}^3$到自身的映射。函数 $\phi$ 要想表示一个旋转，必须在旋转过程中保持向量长度(lengths)、向量夹角(angles)和handedness不变。(handedness和左右手坐标系有关，例如左手坐标系中向量旋转后，仍要符合左手坐标系规则)

1. 长度保持不变要满足：

$\left \|\phi(\mathbf{P}) \right \| = \left \|\mathbf{P} \right\|$

2. 角度不变要满足：

$\phi(\mathbf{P_1})\cdot \phi(\mathbf{P_2}) = \mathbf{P_1}\cdot \mathbf{P_2} \qquad$

3. 最后，handedness保持不变要满足：

$\phi(\mathbf{P_1})\times \phi(\mathbf{P_2})=\phi(\mathbf{P_1}\times\mathbf{P_2}) \qquad$

(未完待续)
可以看3B1B来理解

两个四元数相乘需要16个乘加运算，然而两个3x3矩阵相乘需要27个乘加运算，因此在某些情况下（比如要对同一个对象施加多个旋转变换时），用四元数表示旋转，提高运算效率

分布变换

Warm-up 学习率预热

在预热的小学习率下，模型可以慢慢趋于稳定，等模型相对稳定后再选择预先设置的学习率进行训练，使得模型收敛速度变得更快，模型效果更佳

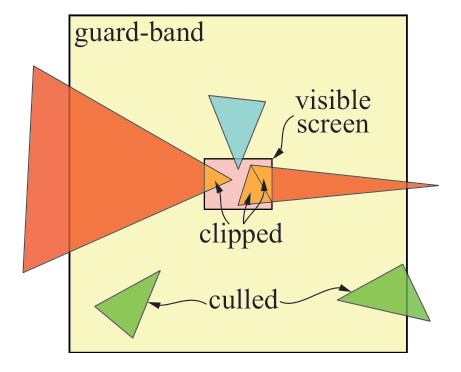
guard band

• 图中粉色的区域是 6500x4900 的屏幕空间，外圈黄色部分是XY轴上+16K~-16K的 guard band。下面的两个绿色三角形，会在三角形准备阶段被剔除掉。最常见的情况是类似蓝色三角形的情况，和屏幕区域相交，但是没有超出 guard-band 区域外，会走正常的 tile 处理流程，不会发生裁剪。红色的三角形，即和屏幕空间相交，又有超出 guard-band区域外的部分，会发生裁剪。注意右边的红色三角形，裁剪时划分成了两个小三角形。
• 由于显卡的帧缓冲是有限的，为了能够支持更大的世界，实际显卡的帧缓冲是支持比 viewport 的帧缓冲大小大得多的的，这个叫做guard band。但是他仍然是有限的，显卡能够处理的三角形也是必须在有限的空间里的（但是三角形的个数可以轻松上亿甚至十几亿），一半 60 帧的引擎同屏渲染几亿三角形应该不在话下。
• 所以实际 CPU 传给 GPU 进行光栅化的三角形空间位置也不能超出视口太多然后还要渲染的，这样的结果是显卡自己处理不了这种三角形，因为他无法访问这么大范围的数据。
• 所以是两阶段裁剪算法：CPU 必须保证所有传送的三角形都在 Guard band 里面。GPU 自己再裁一遍。
  

thread block

• thread: 一个CUDA的并行程序会被以许多个thread来执行。
• block: 数个thread会被群组成一个block，同一个block中的thread可以同步，也可以通过shared memory进行通信。

ablation studies

狭义上的消融实验

在机器学习领域，尤其是复杂的深度神经网络中，"消融研究 "被用来描述切除网络某些部分的过程，以便更好地了解网络的行为。

可以看出，消融实验的目的在于移除系统中的特定的部分，来控制变量式的研究这个部分对于系统整体的影响。如果去除这一部分后系统的性能没有太大损失，那么说明这一部分对于整个系统而言并不具有太大的重要性；如果去除之后系统性能明显的下降，则说明这一部分的设计是必不可少的。当然，如果出现了第三种情况，也就是去除之后模型的性能不降反升，那么建议找一下bug或者修改设计。

广义上的消融实验

我们知道，消融实验的本质上就是控制变量研究单个变量的作用。针对那些无法去除的变量，比如超参数的选择，这时候总不能说让我们把超参数直接去掉来研究它的影响，因此在这种情况下应该应该选择控制系统的其他方面不变，来测试一组超参数来研究这个参数对于系统的影响。因此，超参数调参常用的grid search和random search本质上也是消融实验，它们探究了在只改变一个参数的情况下系统性能的变化从而展示参数对于系统的影响。

gradient flow 梯度流

优化算法中的梯度流与微分方程

参考资料：

协方差矩阵的几何解释