GAMES101作业7 路径追踪(Path Tracing) 问题与思路详解全解

前言

本次作业的内容是对上一次作业中的BVH遍历、射线三角形求交Möller-Trumbore算法进行迁移，以及在此基础上实现完整的 Path Tracing 算法。
请注意： 本次作业基于dalao的GAMES101作业框架，在Windows系统上实现。

函数迁移

Bounds3::IntersectP in Bounds3.hpp

本次作业中 cornell box 模型的墙壁和箱子某些三角形是平行于坐标平面的，会出现包围盒厚度为0的情况，因此求交要包含t_enter = t_exit 的情况。

// in Bounds3.hpp
inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
                                const std::array<int, 3>& dirIsNeg) const
{
    // invDir: ray direction(x,y,z), invDir=(1.0/x,1.0/y,1.0/z), use this because Multiply is faster that Division
    // dirIsNeg: ray direction(x,y,z), dirIsNeg=[int(x>0),int(y>0),int(z>0)], use this to simplify your logic
    // TODO test if ray bound intersects
    float min_x = (pMin.x - ray.origin.x) * invDir[0];
    float max_x = (pMax.x - ray.origin.x) * invDir[0];
    float min_y = (pMin.y - ray.origin.y) * invDir[1];
    float max_y = (pMax.y - ray.origin.y) * invDir[1];
    float min_z = (pMin.z - ray.origin.z) * invDir[2];
    float max_z = (pMax.z - ray.origin.z) * invDir[2];

    if (dirIsNeg[0])
    {
        std::swap(min_x, max_x);
    }

    if (dirIsNeg[1])
    {
        std::swap(min_y, max_y);
    }

    if (dirIsNeg[2])
    {
        std::swap(min_z, max_z);
    }

    float t_enter = std::max(min_x, std::max(min_y, min_z));
    float t_exit = std::min(max_x, std::min(max_y, max_z));

    //包围盒厚度为0时，t_enter = t_exit
    if (t_enter <= t_exit && t_exit >= 0)
    {
        return true;
    }

    else return false;
}

BVHAccel::getIntersection in BVH.cpp

// in BVH.cpp
Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const
{
    // TODO Traverse the BVH to find intersection
    std::array<int, 3Ui64> dirIsNeg = { static_cast<int>(ray.direction.x < 0),static_cast<int>(ray.direction.y < 0),static_cast<int>(ray.direction.z < 0) };;
    if (node->bounds.IntersectP(ray, ray.direction_inv, dirIsNeg) == false)
    {
        return Intersection{};
    }

    if (node->left == nullptr && node->right == nullptr)
    {
        return node->object->getIntersection(ray);
    }

    Intersection hit1 = getIntersection(node->left, ray);
    Intersection hit2 = getIntersection(node->right, ray);

    return hit1.distance < hit2.distance ? hit1 : hit2;
}

Triangle::getIntersection in Triangle.hpp

inline Intersection Triangle::getIntersection(Ray ray)
{
    if (dotProduct(ray.direction, normal) > 0)
    {
        return Intersection{};
    }

    Vector3f s = ray.origin - v0; 
    Vector3f s1 = crossProduct(ray.direction, e2);
    Vector3f s2 = crossProduct(s, e1);

    float de = dotProduct(s1, e1);

    if (fabs(denominator) < EPSILON)
    {
        return Intersection{};
    }

    float coefficient = 1.0f / denominator;
    float t = coefficient * dotProduct(s2, e2);
    float b1 = coefficient * dotProduct(s1, s);
    float b2 = coefficient * dotProduct(s2, ray.direction);
    float b0 = 1.0f - b1 - b2;

    if (t >= 0.0f &&
        b0 >= 0.0f && b0 <= 1.0f &&
        b1 >= 0.0f && b1 <= 1.0f &&
        b2 >= 0.0f && b2 <= 1.0f
        )
    {
        Intersection inter;
        inter.distance = t;
        inter.normal = normal;
        inter.coords = ray(t);
        inter.happened = true;
        inter.m = m;
        inter.obj = this;
        return inter;
    }

    else return Intersection{};
}

Path Tracing

渲染方程 Render Equation:

\Large _{Lo\left( p,\omega _0 \right) \ =\ L_e\left( p,\omega _0 \right) \ +\ \int\limits_{\varOmega +}^{}{L_i\left( p,\omega _i \right) f_r\left( p,w_i,w_0 \right) \left( n\cdot \omega _i \right) dw_i}}

其中第一项表示物体本身的发出的光照强度，第二项的积分所包括的内容就是反射函数 Reflection Equation,即

\Large_{Lo\left( p,\omega _0 \right) \,\,=\,\,\int\limits_{\varOmega +}^{}{L_i\left( p,\omega _i \right) f_r\left( p,w_i,w_0 \right) \cos \theta _idw_i}}

\Large _{Lo\left( p,\omega _0 \right) \,\, =\int\limits_A^{}{L_i\left( p,\omega _i \right) f_r\left( p,w_i,w_0 \right) \frac{\cos \theta _i\cos \theta _{i}^{\prime}}{\lVert x^{\prime}-x \rVert ^2}dA\left( \text{从光源处采样} \right)}}

其中第一项是入射方向的Radiance，代表从单位立体角入射到单位面积上的光照强度。第二项就是双向反射分布函数BRDF(Bidirectional Reflectance Distribution Function) (只与材质有关 $BRDF = Material$ )
，他表示以下比值：

f_r\left( \omega _i\rightarrow \omega _r \right) =\frac{dL_r\left( \omega _r \right)}{dE_i\left( \omega _i \right)}=\frac{dL_r\left( \omega _r \right)}{L_i\left( \omega _i \right) \cos \theta _id\omega _i}\left[ \frac{1}{sr} \right]

蒙特卡洛积分 Monte Carlo Intergration:

\begin{aligned} \int{f\left( x \right) dx=\int{\frac{f\left( x \right)}{p\left( x \right)}p\left( x \right) dx}} =\frac{E\left( f\left( x \right) \right)}{p\left( x \right)} =\frac{1}{N}\sum_{i=1}^N{\frac{f\left( x_i \right)}{p\left( x_i \right)}\left( \text{大数定律} \right)}\text{ } \end{aligned}

采样越多，方差越小

在这里的路径追踪中，我们根据渲染方程着色、利用蒙特卡洛估计离散化、俄罗斯轮盘赌控制深度、重复单次采样来降低方差和减少计算量、从光源处采样来提高效率。

简要地说，就是根据光路可逆原理，从视线(viewpoint)发出一条光线到物体，再①从光源处采样，再追踪这个方向到物体的光线，如果没有遮挡就计算直接光照；②根据材质生成一条任意的wi，有物体相交就是间接光照，递归计算即可，无相交物体或到达光源时停止。

// in Scene.cpp
Vector3f Scene::castRay(const Ray& ray, int depth) const
{
    // TO DO Implement Path Tracing Algorithm here
    //从视线发出光线
	Intersection inter = intersect(ray);

    //没有相交则不需要着色
    if(!inter.happened)
    {
        return Vector3f{ 0.0f, 0.0f, 0.0f };
    }

    //直接返回光源
    if (inter.m->hasEmission())
    {
        if (depth == 0) {
            return inter.m->getEmission();
        }
        else return Vector3f{ 0.0f, 0.0f, 0.0f };
    }
    Vector3f view_dir = ray.direction;
    Vector3f normal = inter.normal.normalized();
    Vector3f position = inter.coords;

    //直接光照和间接光照
    Vector3f L_dir = { 0.0f,0.0f,0.0f }, L_indir = {0.0f, 0.0f, 0.0f};

    //1. 直接光照
    Intersection inter_light;
    float pdf_light;
    //从光源处采样
    sampleLight(inter_light, pdf_light);
    Vector3f normal_light = normalize(inter_light.normal);// NN
    Vector3f position_light = inter_light.coords;// x
    Vector3f light_dir = (position - position_light).normalized();// ws
    float distanceToLight = (position-position_light).norm();
    float distanceToLight2 = dotProduct(position - position_light, position - position_light);// |x - x'|^2
    Ray lightToObj(position_light, light_dir);// Ray(ori,dir)
    Intersection inter_lightToObj = intersect(lightToObj);
    float distanceToObj = inter_lightToObj.distance;
    //利用深度判断是否相交
    //不能用Intersection.happened, 因为一定会和物体相交
    if(inter_lightToObj.happened && distanceToObj - distanceToLight > -EPSILON)
    {
        Vector3f f_r = inter.m->eval(view_dir, -light_dir, normal);
        float cos_theta = dotProduct(-light_dir, normal);// 物体夹角
        float cos_theta_l = dotProduct(light_dir, normal_light); //光源夹角
        L_dir = inter_light.emit*f_r * cos_theta * cos_theta_l / (pdf_light * distanceToLight2);
    }

    //2. 间接光照
    float ksi = get_random_float();
    if(ksi < RussianRoulette)
    {
        //根据材质随机采样一个wi方向
        Vector3f obj_dir = inter.m->sample(view_dir, normal);
        Ray ObjToScene(position, obj_dir);
        Intersection inter_ObjToScene = intersect(ObjToScene);

        if (inter_ObjToScene.happened && !inter_ObjToScene.m->hasEmission())
        {
            Vector3f f_r = inter.m->eval(view_dir, obj_dir, normal);
            float cos_theta = dotProduct(obj_dir, normal);
            float pdf_hemi = inter.m->pdf(view_dir, obj_dir, normal);
        	if (pdf_hemi > EPSILON) {//减少白色噪点
                L_indir = f_r * castRay(ObjToScene, depth + 1) * cos_theta / (pdf_hemi * RussianRoulette);
            }
        }
    }

    return L_dir + L_indir;
}

多线程

在这里运用C++11中的thread可以轻松地分像素进行并行渲染。

// change the spp value to change sample ammount
int spp = 256; // default:16
std::cout << "SPP: " << spp << "\n";

const int thread_cnt = 8;
int finished_thread = 0;
int finished_width = 0;
std::mutex mtx;

printf("%d %d\n", scene.height, scene.width);
auto multiThreadCastRay = [&](uint32_t y_min, uint32_t y_max)
{
    printf("start %d %d\n", y_min, y_max);
    for (uint32_t j = y_min; j <= y_max; ++j) {
        for (uint32_t i = 0; i < scene.width; ++i) {
            // generate primary ray direction
            float x = (2 * (i + 0.5) / (float)scene.width - 1) *
                imageAspectRatio * scale;
            float y = (1 - 2 * (j + 0.5) / (float)scene.height) * scale;

            Vector3f dir = normalize(Vector3f(-x, y, 1));
            for (int k = 0; k < spp; k++) {
                framebuffer[scene.width * j + i] += scene.castRay(Ray(eye_pos, dir), 0) / spp;
            }
        }
        //printf("%d\n", j);
        //UpdateProgress(j / (float)scene.height);
        mtx.lock();
        UpdateProgress(++finished_width * 1.0 / scene.width);
        mtx.unlock();
    }
    printf("ok %d %d\n", y_min, y_max);
};
int block = scene.height / thread_cnt + (scene.height % thread_cnt != 0);
std::thread th[thread_cnt];
for (int i = 0; i < thread_cnt; i++) {
    th[i] = std::thread(multiThreadCastRay, i * block, std::min((i + 1) * block - 1, scene.height));
}
for (int i = 0; i < thread_cnt; i++) th[i].join();
UpdateProgress(1.0);

加速及优化

将Debug更换为Release

Debug 是调试版本，包含调试信息，不优化代码，便于程序员调试；
Release 是发布版本，不包含调试信息，对代码进行优化，便于用户使用。

在图形学中，常常需要进行大量的计算和像素的处理。更换为Release可以大幅提高编译效率，进行更加顺利的测试。

get_random_float() in global.hpp

global.hpp下的get_random_float()随机数生成函数存在问题，它会导致在重复调用该函数时，返回同一个值。

// in global.hpp
static std::random_device dev;
static std::mt19937 rng(dev());
static std::uniform_real_distribution<float> dist(0.f, 1.f); // distribution in range [1, 6]

inline float get_random_float()
{
    return dist(rng);
}

白色噪点

原因应该是pdf接近于0时，除以它计算得到的颜色会偏向极限值，体现在图上也就是白色

要解决这个问题，对于pdf接近于0的情况直接将它的radience算作0就行：

Microfacet微平面理论

这部分内容可以参考LearnOpenGL

BRDF = Material

\large f_r=k_df_{lambert}+k_sf_{cook-torrance}

其中：

$kd$ 是入射光线中被折射部分的能量占比， $ks$ 是被反射部分的能量占比，即菲涅尔项。根据能量守恒定律， $kd+ks=1$ .
$f_{lambert}$ 是Lambertian漫反射（理想散射-郎伯散射）BRDF部分， $f_{cook-torrance}$ 是镜面部分BRDF部分。

Lambertian漫反射

假设物体不吸收能量，由能量守恒得到irradiance入射和出射一定是一样的（ $L_{i}=L_{o}$ ）,因此得到 $f_r=\frac{1}{\pi}$ ;考虑到物体吸收能量的损失后，有：

\large f_{lambert}=\frac{\rho}{\pi}

其中 ${\rho}$ 为反射率或rgb光谱

Cook-Torrance BRDF

\large f\left( l,v \right) =\frac{D\left( h \right) F\left( v,h \right) G\left( l,v,h \right)}{4\left( n\cdot l \right) \left( n\cdot v \right)}

其中:

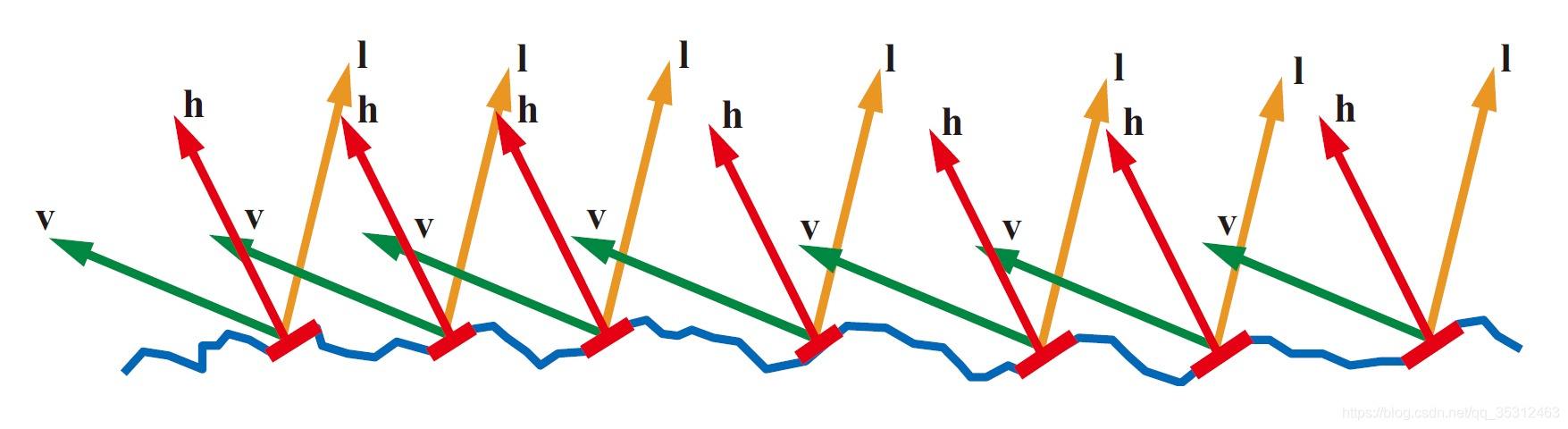
光照方向L,观察方向V, 微观法线/中间向量H,宏观向量N
D(h):法线分布函数(Normal Distribution Function),描述微面元法线分布的概率，即正确朝向的法线的浓度。即具有正确朝向，能够将来自l的光反射到v的表面点的相对于表面面积的浓度。
F(v,h):菲涅尔方程(Fresnel Equation),描述不同的表面角下表面所发射的光线所占的比率。
G(l,v,h):几何函数(Geometry Function),描述微平面自成阴影的属性，即m=h的未被遮蔽的表面点的百分比。
4(n*l)(n*v):校正因子(Correctionfactor),作为微观几何的局部空间和整个宏观表面的局部空间之间变换的微平面量的校正。

一般我们用宏观表面的半矢量h来表示微观表面法线m，因为仅m = h的表面点的朝向才会将光线l反射到视线v的方向，其他朝向的表面点对BRDF没有贡献（正负相互抵消）。

微表面模型需要用到的参数：

$V$ :光线的反射方向(单位向量)
$I$ :光线的入射方向的反方向(单位向量)
$m=h$ : $V$ 和 $I$ 的中间向量(单位向量)
$N$ :为宏观平面法线(单位向量)
${\alpha}$ :为粗糙度∈[0,1]

D(h):法线分布函数(Normal Distribution Function)

各项同性NDF

GGX(Trowbridge-Reitz)分布
GGXT发光的尾部较长，且具备形状不变性。

\alpha =Roughness^2

D_{GGX}\left( \mathbf{m} \right) =\frac{\alpha ^2}{\pi \left( \left( \mathbf{n}\cdot \mathbf{m} \right) ^2\left( \alpha ^2-1 \right) +1 \right) ^2}

Vector3f D_GGXT(Vector3f N,Vector3f H,float rough)
{
    float a = rough * rough;
    float a2 = a * a;
    float NdotH = std::max(dotProduct(N, H), 0.0f);
    float NdotH2 = NdotH * NdotH;

    float denom = (NdotH2 * (a2 - 1.0f) + 1.0f);
    denom = denom * denom;

    return a2 * MY_INV_PI * std::max(denom,0.0000001f);
}

各项异性NDF
创建各向异性NDF的常用方法是基于现有各向同性NDF进行推导。而推导所使用的方法是通用的，可以应用于任何形状不变的各向同性NDF，这便是GGX等形状不变的NDF能更加普及的另一个原因。

Anisotropic GGX分布

D_{GGXaniso}\left( \mathbf{m} \right) =\frac{1}{\pi \alpha _x\alpha _y}\frac{1}{\left( \frac{\left( \mathbf{t}\cdot \mathbf{m} \right)}{\alpha _{x}^{2}}+\frac{\left( \mathbf{b}\cdot \mathbf{m} \right)}{\alpha _{y}^{2}}+\left( \mathbf{n}\cdot \mathbf{m} \right) ^2 \right) ^2}

需要注意的是，将法线贴图与各向异性BRDF组合时，重要的是要确保法线贴图扰动（perturbs）切线和副切线矢量以及法线。

F(v,h):菲涅尔方程(Fresnel Equation)

$v$ 是出射向量，h是中间向量

Schlick Fresnel近似

F_{Schlick}\left( \mathbf{v,h} \right) =F_0+\left( 1-F_0 \right) \left( 1-\left( v\cdot h \right) \right) ^5

float F_Schlick(Vector3f V, Vector3f H,Vector3f F0)
{
    float cos_theta = std::max(dotProduct(V, H), 0.0f);
    return F0 + (1.0f - F0) * std::pow((1 - cos_theta), 5);
}

G(l,v,h):几何函数(Geometry Function)

通常，除了近掠射角或非常粗糙的表面，几何函数对BRDF的形状影响相对较小，但对于BRDF保持能量守恒而言，几何函数至关重要。
在部分游戏引擎和文献中，几何函数G(l,v,h)和分母中的校正因子4（n·l）（n·v）会合并为可见性项（The
Visibility Term），Vis项，简称V项。其也经常作为几何函数的代指：
几何函数与法线分布函数作为Microfacet Specular BRDF中的重要两项，两者之间具有紧密的联系

\large V\left( \mathbf{v,l} \right) =\frac{G\left( \mathbf{l,v,h} \right)}{4\left( \mathbf{n}\cdot \mathbf{l} \right) \left( \mathbf{n}\cdot \mathbf{v} \right)}

几何函数具有两种主要形式：G1和G2，其中：

G1为微平面在单个方向（光照方向L或观察方向V）上可见比例，一般代表遮蔽函数（masking
function）或阴影函数（shadowing function）

G2为微平面在光照方向L和观察方向V两个方向上可见比例，一般代表联合遮蔽阴影函数（joint masking-shadowing
function）在实践中，G2由G1推导而来

默认情况下，microfacet BRDF中使用的几何函数代指G2

\frac{G_2\left( \mathbf{l,v} \right)}{4\left| \mathbf{n}\cdot \left. \mathbf{l} \right|\left| \left. \mathbf{n}\cdot \mathbf{v} \right| \right. \right.}\approx \frac{0.5}{lerp\left( 2\left| \left. \mathbf{n}\cdot \mathbf{l} \right|\left| \right. \left. \mathbf{n}\cdot \mathbf{v} \right|,\left| \left. \mathbf{n}\cdot \mathbf{l} \right|+\left| \left. \mathbf{n}\cdot \mathbf{v} \right|,\alpha \right. \right. \right. \right)}

//G_SchlicksmithGGX_Visibility
float Visibility(Vector3f V,Vector3f L,Vector3f N, float rough)
{
    float NdotV = std::max(dotProduct(N, V), 0.0f);
    float NdotL = std::max(dotProduct(N, L), 0.0f);

    float f = rough + 1.0;
    float k = f * f * 0.125;
    float ggxV = 1.0 / (NdotV * (1.0 - k) + k);
    float ggxL = 1.0 / (NdotL * (1.0 - k) + k);
    return ggxV * ggxL * 0.25;
}

计算误差导致的交点偏离问题
在Intersection getIntersection(Ray ray)函数中修改圆的相交判定，因为圆的相交判定精度不够。
若不修改，程序在运行中会报错，因为当 t0 = 0 时，有可能会造成除0错误。

// in sphere.hpp
Intersection getIntersection(Ray ray) {
    Intersection result;
    result.happened = false;
    Vector3f L = ray.origin - center;
    float a = dotProduct(ray.direction, ray.direction);
    float b = 2 * dotProduct(ray.direction, L);
    float c = dotProduct(L, L) - radius2;
    float t0, t1;
    if (!solveQuadratic(a, b, c, t0, t1)) return result;
    if (t0 < 0) t0 = t1;
    if (t0 < 0) return result;

    if (t0 > 0.5) {//精度不够
        result.happened = true;
        result.coords = Vector3f(ray.origin + ray.direction * t0);
        result.normal = normalize(Vector3f(result.coords - center));
        result.m = this->m;
        result.obj = this;
        result.distance = t0;
    }
    return result;
}

总结：
这个作业还是非常有趣的，让我步入了PBR的大门。但是还有完美镜面反射没有完成，看起来和菲涅尔项、重要性采样有关系，以及伽马校正等视觉效果可以实现，这个以后再说吧。

参考资料：
GAMES101作业7-路径追踪实现过程&代码框架超全解读
 图形学入门笔记3:Path Tracing-Games101作业7
Games101 作业7 绕坑引路 (Windows)
【GAMES101】作业7 常见问题避坑